|
|
|
Graduate SchoolProgram:Saturday the 7th: 10:45 - 11am questions / coffee 12:45 - 1pm questions 3:45 - 4pm questions / coffee 5:45 - 6pm questions 10:45 - 11am questions / coffee 12:45 - 1pm questions 3:45 - 4pm questions / coffee Course 1: After modeling: Turning 3D models into 3D prints
Speaker: Sylvain Lefebvre, InriaAbstract:
With the advent of 3D printing technologies, one could hope that realizing a physical object from a 3D model should be as simple as pushing a button. Unfortunately, for most models this is not true, and the final part is sometimes disappointing in terms of its aesthetics or physical properties. This course will discuss several methods that significantly improve the quality of printed objects and enable novel capabilities through better geometric analysis and modeling of the process constraints.
The challenges of 3D printing are intrinsically linked to the way additive manufacturing technologies operate: by solidification of successive planer layers to form the final object. This discretization is a major source of approximations, turning smooth slanted surfaces into staircases. In addition, the layers are often solidified by filling solid areas along toolpaths, leaving gaps and porosities. With some technologies, solid material can only exist if supported by the layer below, requiring external support structures during fabrication. Beyond the geometric (accuracy) and aesthetic issues, these defects also impact the mechanical properties of the final prints, as well as the time required to produce an object. Bio:
 Sylvain Lefebvre is a senior researcher at Inria (France), where he leads the MFX team. His main research focus is to simplify content creation, synthesizing highly detailed patterns, structures and shapes, with applications in Computer Graphics and additive manufacturing. Sylvain received the EUROGRAPHICS Young Researcher Award in 2010. From 2012 to 2017 he was the principal investigator of the ERC ShapeForge (StG) and IceXL (PoC) projects. He created and is the lead developer of the IceSL software for modeling for additive manufacturing. Sylvain is an active member of the community and has served on the technical papers committee and editorial boards of the main conferences and journals of the field, including EUROGRAPHICS, SIGGRAPH, and Transactions on Graphics. Course 2: Conformal Geometry Processing
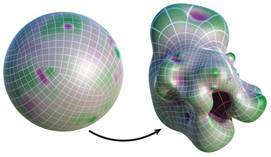
Speaker: Keenan Crane, Carnegie Mellon UniversityAbstract:
Digital geometry processing is the natural extension of traditional signal processing to three-dimensional geometric data. In recent years, methods based on so-called conformal (i.e., angle-preserving) transformations have proven to be a powerful paradigm for geometry processing since (i) numerical problems are typically linear, providing scalability and guarantees of correctness and (ii) conformal descriptions of geometry are often dramatically simpler or lower-dimensional than traditional encodings. Conformal geometry is also linked to constitutive laws appearing in computational mechanics and 3D fabrication. This lecture will touch on both the mathematical foundations of conformal geometry, as well as recent numerical techniques and applications in 3D geometry processing.
Bio:
 Keenan Crane is an Assistant Professor of Computer Science and Robotics at Carnegie Mellon University. His research draws on insights from differential geometry and computer science to develop fundamental algorithms for working with real-world geometric data. He received his BS from UIUC, was a Google PhD Fellow at Caltech, and a NSF Mathematical Sciences Postdoctoral Fellow at Columbia University.Course 3: Robust Geometry Processing
Speaker: Pierre Alliez, Inria Sophia-AntipolisAbstract:
The lack of robustness in current geometry processing software makes it impossible to streamline the processing pipeline. Stringent requirements for input data for the outputs prevent the software building blocks from working together seamlessly. The quest for robustness requires devising algorithms that are reliable on real-world computers (which have inherent imperfections due to finite arithmetic precision). In addition, and in response to the increasing trend for geometry to be acquired through measurements, it requires devising algorithms that are resilient to real-world data. This trend means that the common assumptions applied to input data clash with the practical reality of real-world datasets, which are riddled with imperfections.
In the first part of this tutorial I will briefly review the methods dealing with finite arithmetic precision. I will then review several ideas devised to tackle the resilience to imperfect data, with application to several key problems in geometry processing: reconstruction, approximation, dense correspondence, boolean operations and mesh generation. The ideas covered will include optimal transportation, robust statistics and generalized winding numbers. Bio:
 Pierre Alliez is Senior Researcher and team leader at Inria Sophia-Antipolis - Mediterranee. He has authored many scientific publications and several book chapters on mesh compression, surface reconstruction, mesh generation, surface remeshing and mesh parameterization. He is an associate editor of the Computational Geometry Algorithms Library (http://www.cgal.org). He was awarded in 2005 the EUROGRAPHICS young researcher award. He was co-chair of the Symposium on Geometry Processing in 2008, of Pacific Graphics in 2010 and Geometric Modeling and Processing 2014. He was awarded in 2011-2015 a Consolidator Grant from the European Research Council on Robust Geometry Processing.Course 4: Dynamic 2D/3D Registration
Speaker: Andrea Tagliasacchi, University of VictoriaAbstract:
Image and geometry registration algorithms are an essential component of many computer graphics and computer vision systems. With recent technological advances in RGB-D sensors, such as the Microsoft Kinect or Intel RealSense robust algorithms that combine 2D image and 3D geometry registration have become an active area of research. The goal of this course is to introduce the basics of 2D/3D registration algorithms and to provide theoretical explanations and practical tools to design computer vision and computer graphics systems based on RGB-D devices.
Bio:
 Andrea Tagliasacchi is a visiting professor at Google/Daydream, and an assistant professor at the University of Victoria (Canada) where he holds the Industrial Research Chair in 3D Sensing. Before joining UVic, he was a postdoctoral researcher in the Graphics/Geometry Laboratory at EPFL (Swiss Federal Institute of Technology, Lausanne). He obtained his PhD from Simon Fraser University as an NSERC Alexander Graham Bell scholar, where he worked on digital geometry processing from incomplete data. He received his MSc (cum laude, gold medalist) in digital signal processing from Politecnico di Milano (Italy). His core research interests are real-time modeling and registration, with applications to VR/AR.Course 5: Geometric deep learning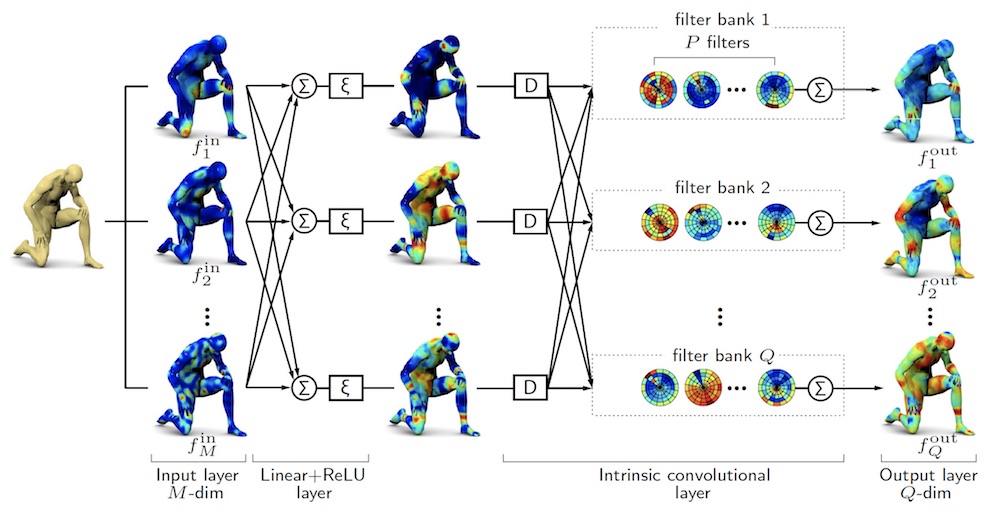
Speaker: Michael Bronstein, University of Lugano and Tel Aviv UniversityAbstract:
The past decade in computer vision research has witnessed the emergence of deep learning, allowing to automatically learn powerful feature representations from large collections of examples. Deep neural networks achieved a breakthrough in performance in a wide range of applications such as image classification, segmentation, detection and annotation. When attempting to apply deep learning to 3D geometric data, one has to face fundamental differences between images and geometric objects. One of the key differences is that in the geometry processing and computer graphics communities, shapes are modeled as manifolds, and one requires to generalize deep neural networks using intrinsic constructions. Intrinsic deep neural networks have recently been used to learn invariant shape features and correspondence, allowing to achieve state-of-the-art performance in several shape analysis tasks, while at the same time allowing for different shape representations, e.g. meshes, point clouds, or graphs.
The purpose of this tutorial is to overview the foundations and the current state of the art in learning techniques for 3D shape analysis and vision. We will overview deep learning techniques for tasks of shape classification, object recognition, retrieval and correspondence. The tutorial will present in a new light the problems of shape analysis, emphasizing the analogies and differences with the classical 2D setting, and showing how to adapt popular learning schemes in order to deal with deformable objects. An emphasis will be made on relation to classical methods in shape analysis, such as spectral descriptors and functional maps.
Bio:
 Michael Bronstein (PhD with distinction 2007, Technion, Israel) is a professor at USI Lugano, Switzerland and Tel Aviv University, Israel. He also serves as a Principal Engineer at Intel Perceptual Computing. During 2017-2018 he is a fellow at the Radcliffe Institute for Advanced Study at Harvard University. Michael's main research interest is in theoretical and computational methods for geometric data analysis. He authored over 150 papers, the book Numerical geometry of non-rigid shapes (Springer 2008), and over 20 granted patents. He was awarded three ERC grants, two Google Faculty Research awards (2015, 2017), and Rudolf Diesel fellowship (2017) at TU Munich. He was invited as a Young Scientist to the World Economic Forum, an honor bestowed on forty world’s leading scientists under the age of forty. Michael is a Senior Member of the IEEE, alumnus of the Technion Excellence Program and the Academy of Achievement, ACM Distinguished Speaker, and a member of the Young Academy of Europe. In addition to academic work, Michael is actively involved in commercial technology development and consulting to start-up companies. He was a co-founder and technology executive at Novafora (2005-2009) developing large-scale video analysis methods, and one of the chief technologists at Invision (2009-2012) developing low-cost 3D sensors. Following the multi-million acquisition of Invision by Intel in 2012, Michael has been one of the key developers of the Intel RealSense technology.Course 6: Model Reduction for Shape Deformation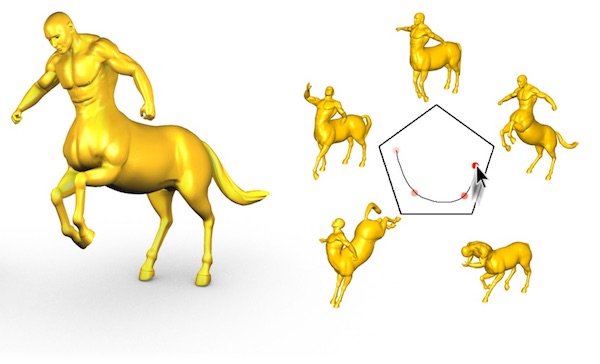
Speaker: Klaus Hildebrandt, TU DelftAbstract:
Shape deformation problems are at the heart of many geometry processing tasks, such as shape editing, template-based capture, shape optimization, computational design and elastic simulation. The applications place high demands on the solvers for these problems. On the one hand, the shapes to be deformed are complex and deformations can be large, hence large scale non-linear problems need to be solved, on the other hand, computations need to be fast, e.g., for interactive applications. In this lecture, we will learn about model reduction techniques and how they can be used to design fast approximation algorithms for certain types shape deformation problems.
Bio:
 Klaus Hildebrandt is a faculty member at the Intelligent Systems Department at Delft University of Technology, The Netherlands. Previous to that he was a Senior Researcher at the Max Planck Institute for Informatics in Saarbrücken, Germany, where he headed the Applied Geometry group. He received his PhD in mathematics from Freie University Berlin. His research interests are in geometric modeling and geometry processing, computational and discrete differential geometry and physics-based computer animation. His work received several best paper awards at international conferences including Eurographics, ACM UIST, Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, and Solid Modeling International. He has co-chaired the Symposium on Geometry Processing in 2017 and the Eurographics STAR program in 2018Course 7: Computational Optimal Transport
Speaker: Bruno Levy, Inria-Nancy Grand-EstAbstract:
This course gives an introduction to optimal transport, a mathematical theory that makes it possible to measure distances between functions (or distances between more general objects), to interpolate between objects or to enforce mass/volume conservation in certain computational physics simulations. Optimal transport is a rich scientific domain, with active research communities, both on its theoretical aspects and on more applicative considerations, such as geometry processing and machine learning. This course aims at explaining the main principles behind the theory of optimal transport, introduce the different involved notions, and more importantly, how they relate, to let the reader grasp an intuition of the elegant theory that structures them. After presenting several state-of-the-art algorithms to solve this problem on a computer, I will show some applications in computational physics (fluid simulation and astrophysics).
Bio:
 Bruno Levy is a researcher with Inria, where he leads the ALICE project-team. He currently works on some geometry-related problems in scientific computing and computational physics, including mesh generation, sampling, and solving PDEs, with applications in mechanics, fluid dynamics and astrophysics. Before then (2000-2006), he worked on mesh parameterization and some of its applications in computer graphics, including texture mapping. He is associate editor of ACM TOG, The Visual Computer and Graphical Models. He obtained two ERC grants, one in 2008 (StG-GOODSHAPE) and one in 2013 (PoC-VORPALINE). In 2011 he received the Inria young researcher award. Most of his research results from 2000 to now are available in his open-source Geogram and Graphite softwares. |
| Online user: 1 | RSS Feed |
|
